https://youtu.be/uJryes5Vk1o?si=H8dxie1J-nK_tLv-
로지스틱 회귀 모델과 단일 훈련 샘플이 얼마나 잘 작동하는지 측정하는 손실 함수, 그리고 매개변수 $w$, $b$가 훈련 세트 전체를 얼마나 잘 예측하는지 측정하는 비용 함수에 대해서 알아보았습니다. 그러면 이제 경사 하강법 알고리즘을 사용해 매개변수 $w$와 $b$를 훈련 세트에 학습시키는 방법을 알아봅시다.
$\hat{y} = \sigma(w^Tx+b), \quad\sigma(z)=\frac{1}{1+e^{-z}}$
$\mathcal{J}(w,b)=\frac{1}{m}\sum^{m}{i=1}\mathcal{L}(\hat{y}^{(i)},y^{(i)})=-\frac{1}{m}\sum^{m}{i=1}y^{(i)}\log\hat{y}^{(i)}+(1-y^{(i)})\log(1-\hat{y}^{(i)})$
전에 배웠던 로지스틱 회귀 알고리즘입니다. 두 번째 줄에는 비용 함수 $\mathcal{J}$가 있습니다. 매개변수 $w$와 $b$에 대한 함수이죠. 이는 평균으로 정의할 수 있으므로 $\frac{1}{m}$에 손실 함수의 합을 곱합니다. 손실 함수는 알고리즘이 각 훈련 샘플의 $\hat{y}$이 얼마나 좋은지를 참값 $y^{(i)}$와 비교해 측정합니다. 오른쪽에는 전체 식을 전개해 놓았습니다.
비용 함수는 매개변수 $w$와 $b$가 훈련 세트를 잘 예측하는지 측정합니다. 그러면 매개변수 $w$와 $b$를 알아내기 위해서는 비용 함수 $\mathcal{J}(w, b)$를 가장 작게 만드는 $w$와 $b$를 찾아야 할 것입니다.
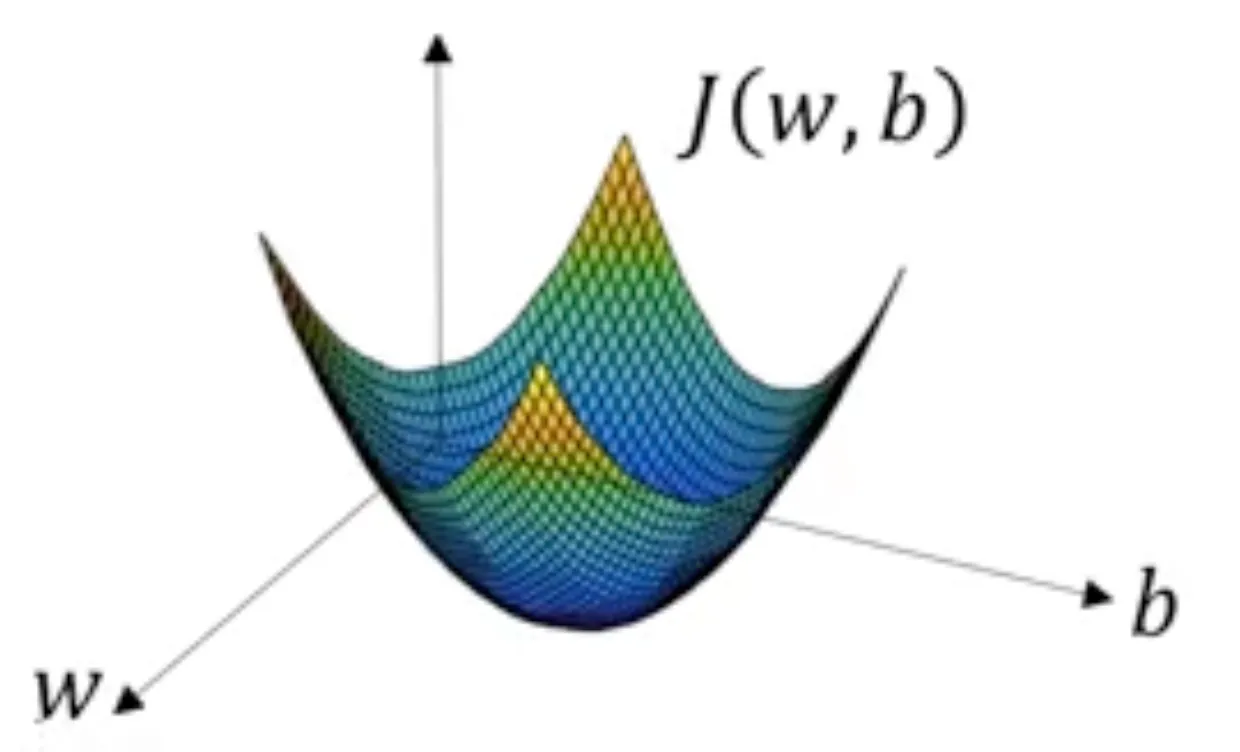
경사 하강법을 그려보면 이렇습니다. 이 그래프에서 두 가로축은 매개변수 $w$와 $b$의 공간을 나타냅니다. 실제로는 $w$가 더 높은 차원을 취할 수도 있지만, 도표를 그릴 때는 $w$와 $b$를 각각 하나의 실수라고 가정하였습니다. 그러면 비용 함수 $\mathcal{J}(w, b)$는 가로축 $w$, $b$ 위의 곡면이고, 곡면의 높이는 그 점의 $\mathcal{J}(w, b)$ 값을 나타냅니다.

여기서 비용 함수 $\mathcal{J}$의 최솟값에 해당하는 $w$와 $b$를 찾아야 합니다. 이 특정 비용 함수 $\mathcal{J}$는 활처럼 볼록한 함수(위)입니다. 볼록하지 않은 함수는 이런 함수(아래)로서 지역 최적값이 여러 개입니다. 이 비용 함수 $\mathcal{J}(w, b)$가 볼록하다는 사실이 로지스틱 회귀에 위의 비용 함수 $\mathcal{J}$를 사용한 큰 이유 중 하나입니다.

매개변수에 쓸 좋은 값을 찾기 위해서 $w$와 $b$를 어떤 초깃값으로 초기화해야 합니다. 이는 여기 빨간 점으로 나타내겠습니다. 로지스틱 회귀에는 거의 모든 초기화 방법을 사용할 수 있는데, 보통 초깃값을 0으로 설정합니다. 무작위 초기화도 가능하지만 보통 로지스틱 회귀에는 사용하지 않습니다. 하지만 이 함수는 볼록하기 때문에 어디서 초기화를 해도 거의 같은 점에 도착하게 될 것입니다.
경사 하강법에서는 이 초기점에서 시작해 가장 가파른 내리막 방향으로 한 단계 내려갑니다. 그러면 한 단계 후에 이쯤에 오게 될 것입니다. 경사 하강법을 한 번 반복하면 이렇게 되고, 두 번 반복하면 이렇게, 세 번째는 이럴 것이고, 그러다가 언젠가 전역 최적값이나 그 근사치에 도달하게 될 것입니다.
경사 하강법을 이런 그림으로 나타내 보았는데 좀 더 세부적인 것들을 적어보도록 하겠습니다.
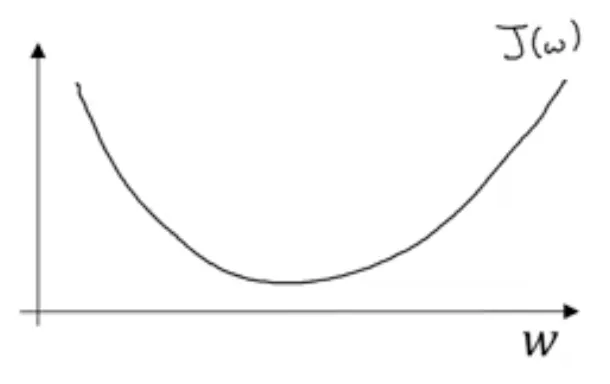
예를 들어 이렇게 생긴 함수 $\mathcal{J}$를 최소화한다고 해 봅시다. 그리기 쉽도록 잠깐 $b$를 제외해 높은 차원이 아니라 1차원으로 생각해 봅시다.
경사 하강법은 계속해서 $w$의 값을 갱신합니다. $:=$는 값을 갱신한다는 뜻입니다. $w$를 $w - α$에 $\mathcal{J}(w)$의 미분계수 $\frac{d\mathcal{J}(w)}{dw}$를 곱한 값으로 갱신하고, 이를 알고리즘이 수렴할 때까지 반복합니다. 여기서 $α$는 학습률이고, 경사 하강법을 반복할 때 한 단계의 크기를 결정합니다.
이것은 미분계수입니다. 갱신할 때 매개변수 $w$에 줄 변화를 나타냅니다. 경사 하강법을 구현하는 코드를 만들 때는 관습적으로 이 미분계수의 변수 이름을 $dw$라고 정합니다. 예를 들면 코딩을 할 때 w := w - α * dw라고 쓰는 것이죠.

이 경사 하강법이 잘 작동하는지 확인해 봅시다. $w$가 여기(오른쪽) 있고 그에 따라 $\mathcal{J}(w)$도 여기 있다고 해 봅시다. 미분계수는 이 점에서 함수의 기울기라고 정의할 수 있습니다. 기울기는 $\mathcal{J}(w)$에 접선하는 삼각형의 세로/가로라고 할 수 있죠. 이 점의 미분계수는 양수입니다. $w$는 $w$ - 학습률 x 미분계수로 갱신되는데, 미분계수가 양수이므로 $w$에서 미분계수를 빼는 것이 되어서 왼쪽으로 한 단계 갑니다.
반대로 $w$가 여기(왼쪽) 있었다면 기울기 $\frac{d\mathcal{J}(w)}{dw}$는 음수가 되고, $α$에 음수를 곱한 값을 빼게 되므로 서서히 $w$를 증가시키게 됩니다. 각 반복마다 $w$가 점점 증가하는 것입니다. 그러면 왼쪽에서 초기화하던, 오른쪽에서 초기화하던, 경사 하강법은 매개변수를 전역 최솟값까지 도달하게 해 줍니다.
도함수에 대해서 잘 알지 못하고 $\frac{d\mathcal{J}(w)}{dw}$가 무슨 뜻인지 모른다면 다음 동영상에서 알아 볼 테니 크게 걱정하지 않아도 됩니다. 이미 미적분에 대해 잘 알고 있다면 신경망이 어떻게 작동하는지 더 깊은 직관을 가질 수 있을 것이고, 미적분에 익숙하지 않더라도 추후 동영상에서 미적분과 도함수에 대해 충분한 직관을 얻어 이를 신경망에 효과적으로 적용할 수 있게 될 것입니다.
지금은 이 항이 함수의 기울기를 나타낸다고만 알면 됩니다. 그리고 현재 매개변수 위치에서 함수의 기울기를 찾아, 가장 가파른 경사로 내려가는 각 단계에 적용함으로써 비용 함수 $\mathcal{J}$에서 내려가는 방향을 찾을 수 있습니다.
여태까지 매개변수가 $w$만 있을 경우인 $\mathcal{J}(w)$에 대한 경사 하강법을 알아보았습니다. 로지스틱 회귀에서 비용 함수는 $w$와 $b$에 대한 함수이고, 그런 경우 경사 하강법의 내부 반복문은 다음과 같이 바꿀 수 있습니다.
$w$는 $w-α\frac{d\mathcal{J}(w,b)}{dw}$, $b$는 $b-α\frac{d\mathcal{J}(w,b)}{db}$로 갱신합니다. 구현할 때 사용하게 될 식은 밑에 있는 두 식입니다.
w := w - α(dJ(w,b)/dw)
b := b - α(dJ(w,b)/db)
잠시 미적분에서 사용하는 표기법 하나를 알아 봅시다. 헷갈려 하는 사람이 꽤 있을 것입니다. 미적분을 이해하는 것이 아주 중요하다고 생각하지는 않지만 이것을 보고 헷갈리는 일이 없었으면 합니다.
바로 이 항을 이렇게 $\partial$를 사용해 쓰는 것입니다. 이 $\partial$는 소문자 $d$를 다른 폰트로 쓴 것뿐인데, 이것은 단순히 $\mathcal{J}(w, b)$의 미분계수를 의미합니다. 그러니까 $\mathcal{J}(w, b)$가 $w$ 방향으로 얼마나 기울었는지를 나타냅니다.
미적분에서 이 표기는 완벽히 논리적이지도 않고 복잡하기만 한 것 같지만, $\mathcal{J}$가 두 개 이상의 변수를 가진 함수일 때 $d$ 대신 사용합니다. 이 기호는 편미분 기호라고 하는데, 크게 신경 쓸 필요는 없습니다. $\mathcal{J}$가 변수가 하나인 함수라면 그냥 소문자 $d$를 사용합니다.
따라서 편미분 기호 와 소문자 $d$의 차이는 $\mathcal{J}$가 두 개 이상의 변수를 가진 함수면 이 편미분 기호 $\partial$를, $\mathcal{J}$가 하나의 변수를 가진 함수이면 소문자 $d$를 사용하는 것입니다.
이것은 미적분에서 사용하는 특이한 표기법 중 하나인데, 제 생각에는 필요 이상으로 복잡해지기만 하는 것 같습니다. 어쨌든 편미분 기호를 보면 여러 변수 중 하나에 대한 함수의 기울기를 구하는 것이라고 알면 됩니다.
그래서 정확하게 미적분의 표기법을 따르려면 여기 밑에 있는 $\mathcal{J}$의 변수는 두 개니까 편미분 기호를 사용해야 합니다. 그래도 의미는 소문자 $d$와 거의 똑같습니다.
마지막으로 코드 구현 시 관습적으로 $w$의 변화를 나타내는 $\frac{d\mathcal{J}(w,b)}{dw}$ 값은 변수의 이름을 dw라 하고, $b$의 변화량을 나타내는 $\frac{d\mathcal{J}(w,b)}{db}$ 값은 db라 합니다.
좋습니다. 경사 하강법은 이렇게 구현하는 것이고, 미적분을 공부한지 꽤 되었다면 감당할 수 있는 이상으로 미적분이 많이 나온다고 생각할 수 있는데, 그렇게 생각한다면 다음 동영상에서 미분에 대해 더 나은 직관을 얻을 수 있을 것입니다.
미적분에 대한 깊은 수학적 지식 없이 직관적으로 이해하는 것만으로도 신경망을 효율적으로 만들 수 있게 될 것입니다. 그러면 다음 동영상에서 미분에 대해 더 알아보겠습니다.




댓글