Basic Concept 기본 개념
벡터는 길이와 방향을 동시에 가진다. 요소의 개수에 따라 차원이 결정되고, 변형이 허용되는 벡터는 자유벡터(free vector), 시작점이 원점에 고정되어 변형이 제한되는 벡터는 고정벡터(fixed vector, bound vector)라고 한다.
Basic Operation 기본 연산
길이, 크기 (length)
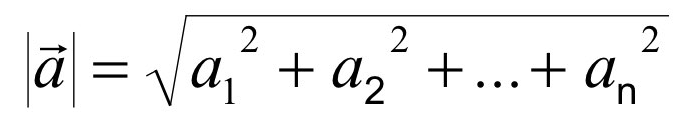
방향 (direction)
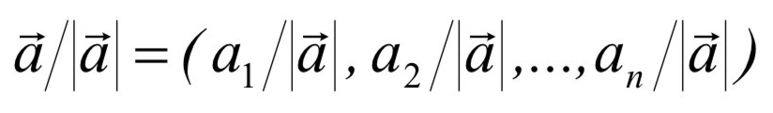
스칼라 연산
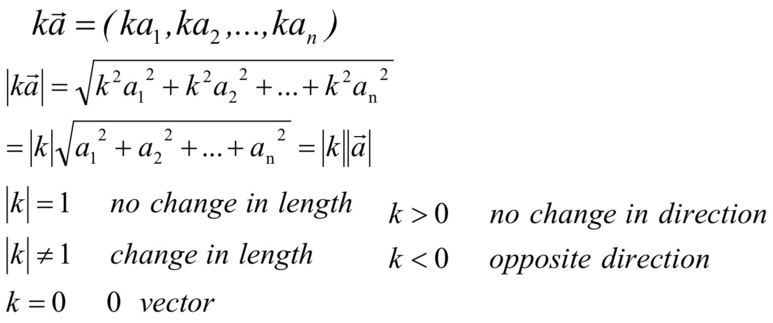
덧셈

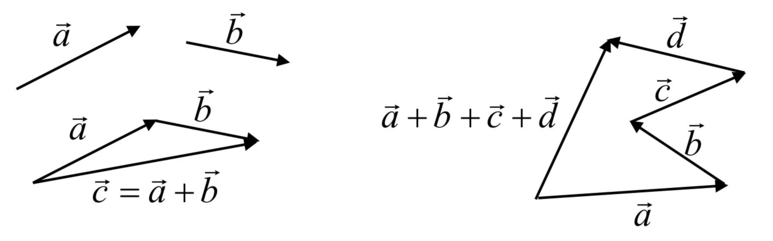
평행사변형 (parellelogram) 법칙 :
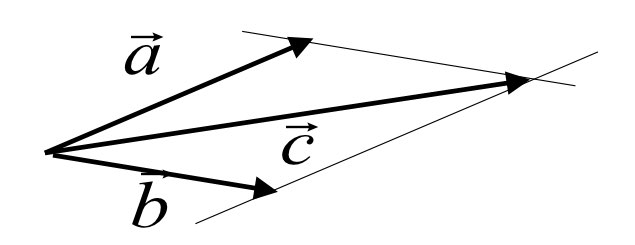
뺄셈
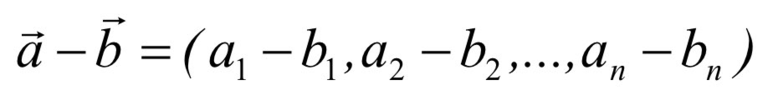
교환 (commutative), 결합 (associative), 분배 (distributive) 법칙
벡터의 덧셈과 뺄셈, 스칼라곱 연산에서는 교환법칙, 결합법칙, 분배법칙이 모두 성립한다.
Dot Product 내적
Dot Product, 내적 연산은 Scalar Product로도 불리는데, 계산 결과가 스칼라 값으로 나오기 때문이다.
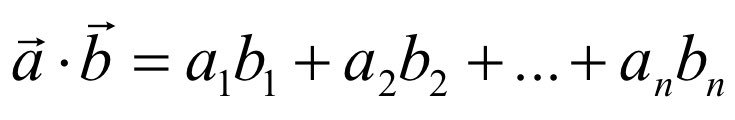
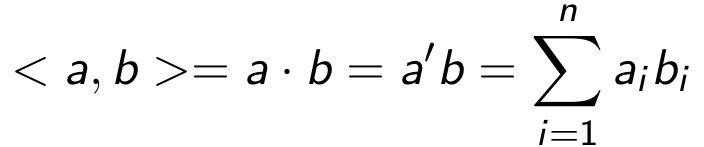
내적 연산은 교환법칙, 결합법칙, 분배법칙이 성립한다. 내적 연산을 활용한 연산 중에서 기억할만한 연산은 다음과 같다.
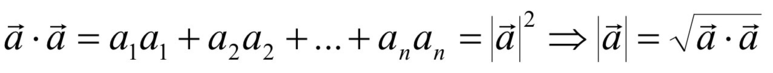
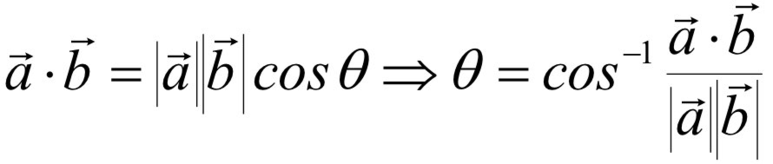
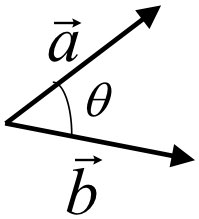
두 벡터를 내적한 결과가 0이라면 두 벡터는 수직 하며, 이 명제의 역도 성립한다.
Cross Product 외적
Cross Product, 외적 연산은 Vector Product로도 불리는데, 계산 결과가 벡터 값으로 나오기 때문이다.
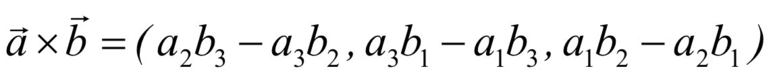
외적 연산은 교환법칙이 성립하지 않는다.
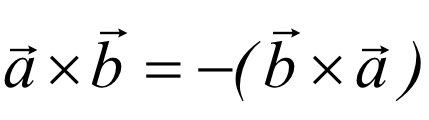
벡터 a와 b를 외적한 결과 벡터 c는 벡터 a와 b 둘 다에 수직 하다.
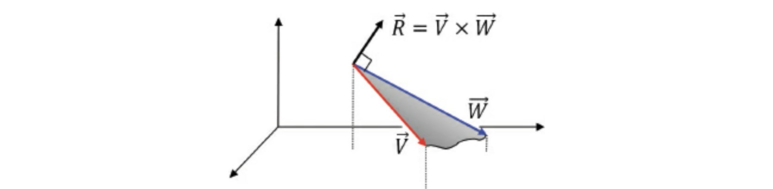
외적 되는 두 벡터 사이의 각을 θ라고 할 때, 다음과 같은 공식 도출이 가능하다.
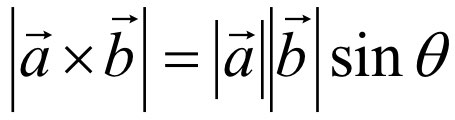
두 벡터가 평행할 때, 외적 결과는 0이다.
Norm 노름, 놈
노름은 벡터의 길이(크기)를 표현하는 방법 중 하나이다. 4차원 이상의 벡터 크기도 계산이 가능하다.
||a|| = root(a'a) = length of a
예를 들어,
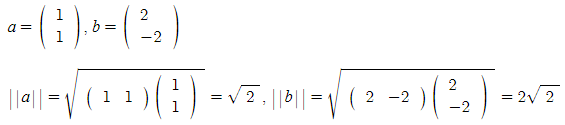
Vector Space 벡터 공간
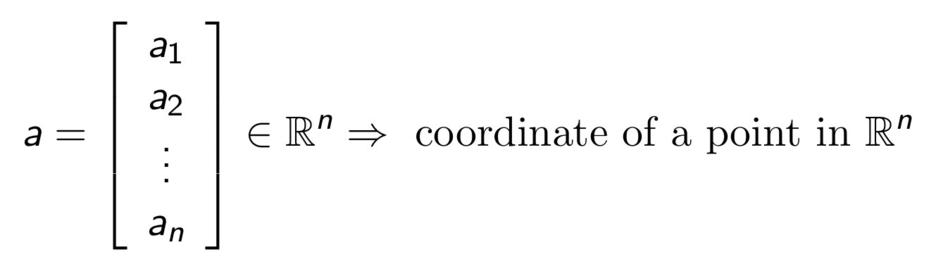
V is a vector space if and only if ∀v, x ∈ V and α, β ∈ (실수체), we have αx + βy ∈ V, i.e., it is closed under scalar multiplication and addition.
벡터 공간은 원소를 서로 더하거나 주어진 배수로 늘이거나 줄일 수 있는 공간이다. 벡터 공간의 원소를 벡터라고 하며, 이는 직관적으로 방향 및 길이의 비가 정의된 대상을 나타낸다. (노름(길이)이 주어지지 않은 일반적인 벡터 공간에서는 벡터의 길이 자체는 정의 X) *출처 : 위키백과
Span 스팬
2차원 실수체에 존재하는 임의의 벡터 x, y가 linearly independent 할 때, 둘의 선형 결합(linear combination)으로 2차원 실수체에 존재하는 모든 벡터를 표현할 수 있다. 이러한 경우에 두 벡터 x, y 는 2차원 공간(R^2)을 스팬(span)한다.
A set of vectors, {v1, v2, ..., vn} in a vector space V is said to span V if and only if ∀v ∈ V , there exist α1, ..., αn ∈ R such that v = ∑i=1^n αivi .
Linearly Independent
linearly dependent 한 관계를 선형 종속, linearly independent 한 관계를 선형 독립이라고 한다. 이것은 두 개 이상의 벡터 집합이 서로 선형적으로 종속된 관계인지, 독립된 관계인지를 일컫는 방식이다.
어떠한 벡터들(x1, x2, x3, ..., xn)이 서로 linealy independent, 즉 선형 독립 관계라면, 상수 a1, a2, a3, ..., an의 값이 모두 0일 때만 다음 식을 만족한다.

0이 아닌 non-zero 솔루션이 있다면, 해당 집합의 모든 벡터들은 linearly dependent, 선형 종속 관계이다.
예를 들어, x1 = (1, 0), x2 = (0, 1), x3 = (1, 1)일 때, a1(1, 0) + a2(0, 1) + a3(1, 1) = (a1 + a3, a2 + a3) = 0을 만족하려면 a1 = a2, a3 = - a1 이므로, a1 = a2 = a3 = 0 인 경우 말고도, a1 = a2 = 1, a3 = -1 인 non-zero 솔루션이 존재하기 때문에 x1, x2, x3는 linearly dependent 하다.
Dimension and Basis 벡터 공간의 차원과 Basis
dim(V) = dimension of V = the smallest number of vectors that span V
벡터 공간의 차원은 linearly independent 한 벡터 조합 subset의 최대 크기 (즉 linearly independent한 벡터의 개수가 차원의 크기가 된다.)
바로 전 linealy independent의 예시에서, x1, x2, x3는 linearly dependent 했지만, {x1, x2, x3}의 subset {x1, x2}는 linearly independent 하다. 따라서 {x1, x2, x3}의 벡터 공간 차원은 linearly independent 한 subset {x1, x2}의 크기인 2차원이 된다.
Basis : A set of vectors that span V and that are linearly independent is said to be a basis of the vector space V.
Span 되는 Vector 공간을 만드는 linearly independent 한 벡터들(subset을 구성하는 벡터들)을 기저벡터(basis vector)라고 한다.
Coordinate System 좌표계
linearly independent한 기저 벡터들의 개수만큼, n차원의 좌표계를 만들 수 있다. 그리고 이렇게 만들어진 좌표계 상에 모든 점은 기저벡터의 선형 조합으로 나타낼 수 있다.
예를 들어, 다음 그림은 기저벡터 e1방향으로 a칸, 기저벡터 e2방향으로 b칸 이동한 위치 (a, b)에 존재하는 벡터 a를 선형 조합으로 나타내는 방법이다.
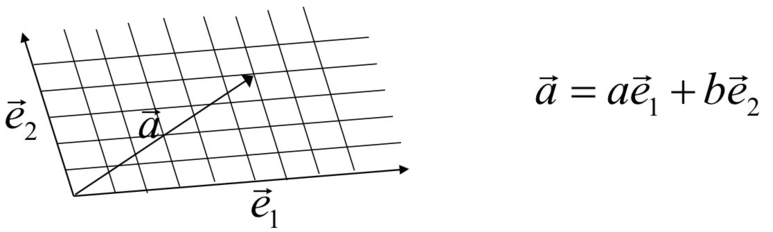
만약 기저벡터가 단위벡터인 (0, 1), (1, 0)이라면, 우리가 흔히 알고 있는 좌표계가 생성되며, 이를 데카르트 좌표계(Cartesian Coordinate System)라고 한다. 물론, 이 좌표계 상에 점도 기저벡터인 단위벡터들의 선형조합으로 표현된다.


'College Study > OpenGL' 카테고리의 다른 글
| [그래픽스] 파일에서 GLSL 소스코드 읽기 (0) | 2020.06.08 |
|---|---|
| [그래픽스] OpenGL과 GLSL의 오류 검출 (0) | 2020.06.08 |
| [그래픽스] Shader (쉐이더) (0) | 2020.06.04 |
| [그래픽스] OpenGL 프로그램 개요 (1) | 2020.06.01 |
| [그래픽스] 컴퓨터 그래픽스 프로그래밍 개발 환경 구축 (Windows, MacOS) (3) | 2020.05.22 |




댓글