* Computer Graphics Programming in OpenGL with C++ 책을 참고하였습니다.
* 책을 번역한 것이 아닌, 제가 독학 후 책을 참고하여 설명하는 게시물입니다. 따라서 책에 없는 부연 설명이 있기도 하며, 의역 또는 오역, 오개념이 있을 수 있습니다. 피드백은 댓글을 남겨주세요.
* 영어 용어를 최대한 한국어로 번역하지 않습니다. 처음부터 코드에서 사용되는, 또는 원서나 인터넷에서 사용되는 보편적 용어를 사용하여 개념을 잡는 것을 추천드립니다.
Local Space
OpenGL 또는 다른 프레임워크들로 3D 그래픽스를 사용하는 목적은 주로 3차원의 세상을 구현하고 그 속에 오브젝트를 배치하여 모니터로 보는 것입니다. 3D 오브젝트 모델을 처음 생성할 때에는, 모델을 가장 편리한 방법으로 배치하기 마련입니다. 예를 들어, 구를 만들 땐 구의 중심의 좌표를 (0,0,0)으로 설정하고, 반지름을 간단하게 (예를 들어, 1) 설정합니다. 이렇게 모델이 정의되는 공간을 Local Space라고 부릅니다. (Model Space라고 하기도 하며, OpenGL 도큐먼트는 이를 Object Space라고 부릅니다.)
각각의 Local Space에서 정의된 모델들은 더 큰 모델의 일부분으로 사용될 수 있습니다. 예를 들어, 위에서 정의된 구가 로봇의 머리가 될 수 있죠. 물론 그 로봇은 고유의 Local Space 내에서 정의될 것입니다. 구를 로봇의 일부분으로서 사용하기 위해서는, 변환 행렬을 사용하여 적절히 배치 및 조절이 되어야 합니다. 이러한 방식으로, 복잡한 모델은 계층적으로(hierarchically) 만들어질 수 있습니다.
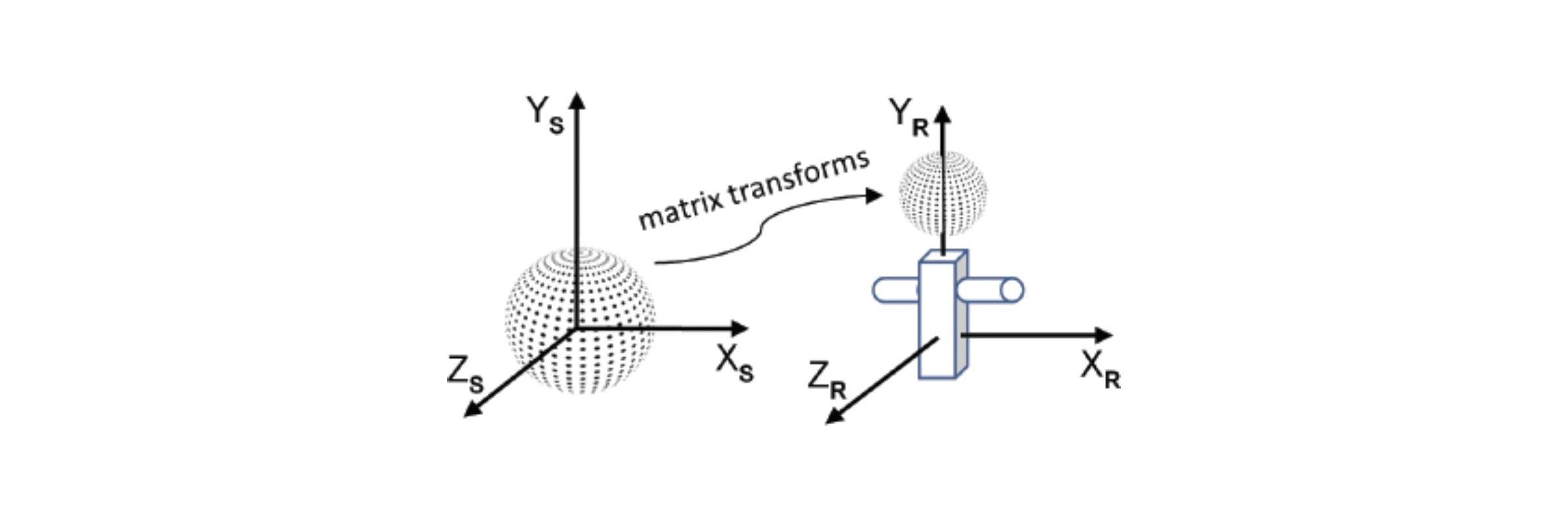
World Space
모델링된 오브젝트들은 3차원의 세상에 배치됩니다. 모든 오브젝트들이 배치되는 공간인 이 3차원 세상을 World Space라고 부릅니다. 오브젝트를 World Space에 배치하고 방향을 지정하는 행렬을 Model Matrix 또는 M이라고 합니다.
Eye Space
지금까지의 변환 행렬들은 모두 3D 공간에서 적용되는 행렬입니다. 하지만 우리는 3D 공간을 (또는 그 일부를) 궁극적으로 2D 모니터에 보여지도록 해야 합니다. 그러기 위해서는, 일단 vantage point를 설정해야 합니다. vantage point는 우리가 현실에서 세상을 '눈'이라는 특정한 지점에서 바라보듯이, 가상 3D 공간을 특정 위치에서 특정 방향으로 바라보는 지점을 말합니다. 이 vantage point를 View Space 또는 Eye Space라고 하며, Synthetic Camera라고 하기도 합니다.
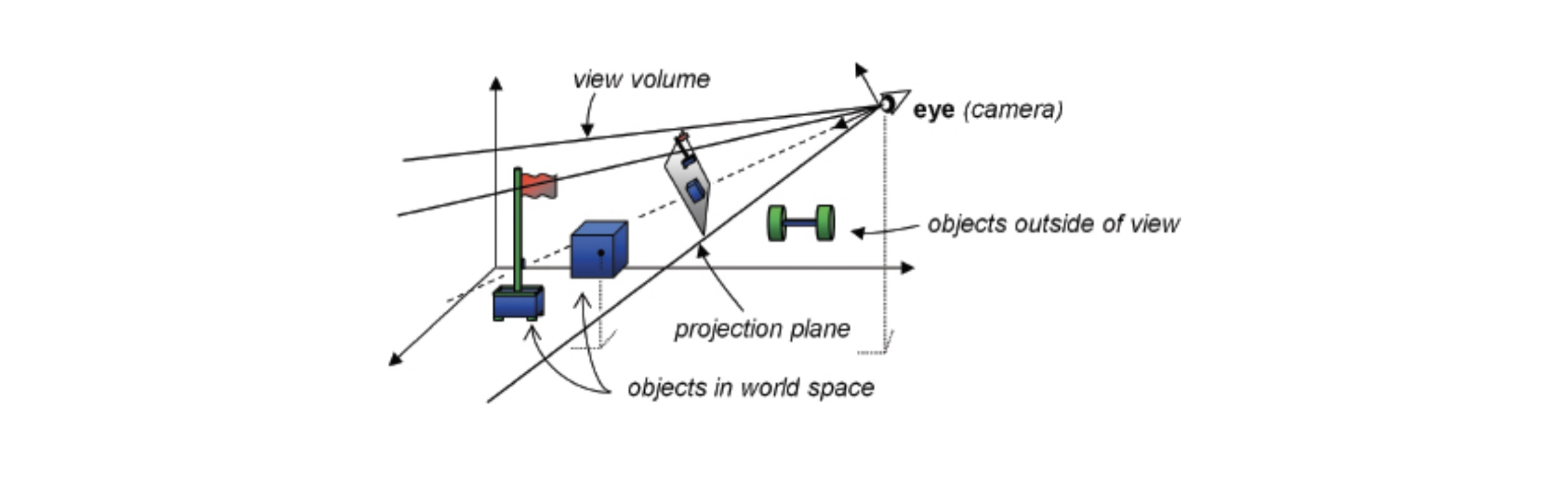
Viewing
1. 카메라를 world space의 특정 location에 배치합니다.
2. 카메라의 방향을 설정합니다. (이 카메라는 보통 고유의 직교하는 축 U, V, N을 유지합니다.)
3. view volume을 정의합니다.
4. volume 속 오브젝트들을 projection plane 위에 투영(project)합니다.
Camera Space of OpenGL
OpenGL은 영구적으로 원점 (0,0,0)에 고정되고, Z축의 음의 방향을 바라보는 카메라를 포함합니다. 이 카메라를 사용하려면, 원하는 위치와 방향으로 카메라를 이동시키는 것처럼 계산해야 합니다. 바로, World Space에서 원하는 카메라 위치와 상대적으로 배치된 오브젝트의 위치를 계산하는 것입니다. 그러면 오브젝트가 World Space가 아닌 카메라로부터의 상대적 위치를 표현 가능한 Camera Space에 위치하게 되는 것입니다.
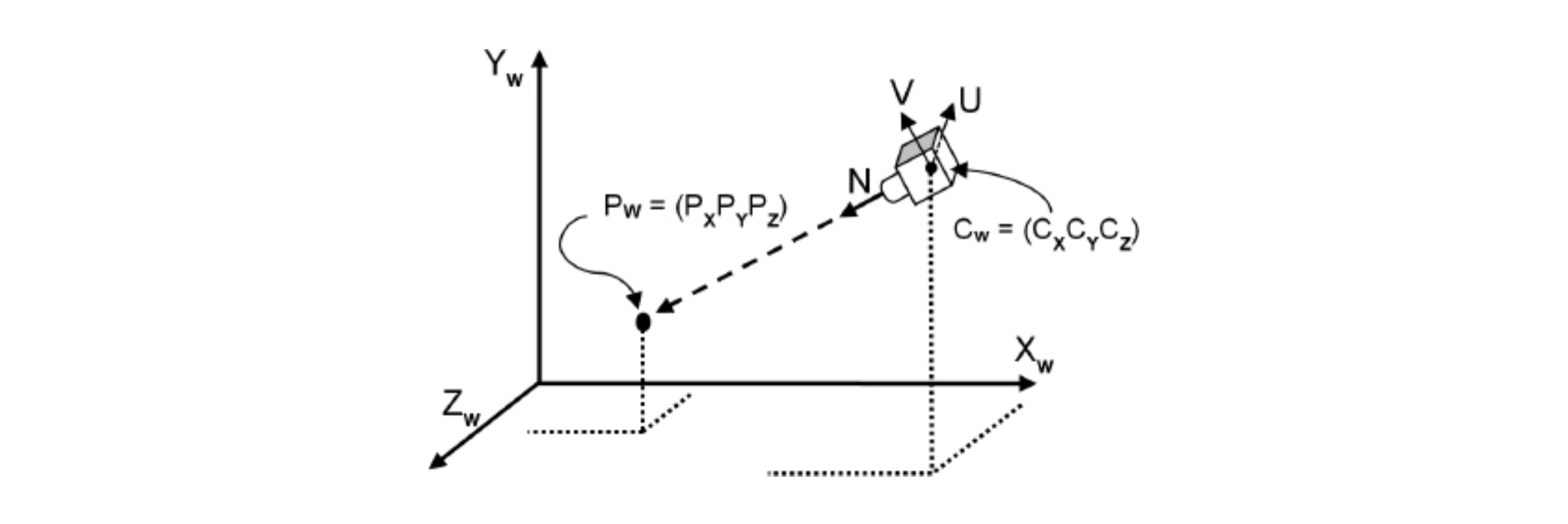
1. Pw를 원하는 카메라 위치의 부호를 반대로 한 값으로 traslate합니다.
2. Pw를 원하는 카메라 방향 오일러 각의 부호를 반대로 한 값으로 rotate합니다.
* World Space에서 Pw에 대해 카메라가 갖는 상대적인 위치, 방향을 반대로 Pw에 적용시킨다는 의미입니다. OpenGL은 카메라의 위치가 고정되어있고, 이 카메라에 대해 오브젝트(Pw)가 갖는 상대적 위치, 방향을 계산해 Camera Space를 정의하기 때문입니다. 이해를 돕기 위한 원문은 아래와 같습니다.
1. Translate Pw by the negative of the desired camera location.
2. Rotate Pw by the negative of the desired camera orientation Euler angles.
translation 행렬 T(원하는 카메라의 위치의 부호를 반대로 한 값을 포함하는 행렬)와 rotation 행렬 R(원하는 카메라의 방향의 부호를 반대로 한 값을 포함하는 행렬)을 연결하여 viewing transform 행렬 V를 만들 수 있습니다. 이는 행렬 간 결합법칙이 성립하기 때문입니다. 식은 오른쪽부터 계산됩니다. Pw를 translation한 후 rotation을 하면 다음과 같습니다.
Pc = R * ( T * Pw )
Pc = ( R * T ) * Pw
Pc = V * Pw
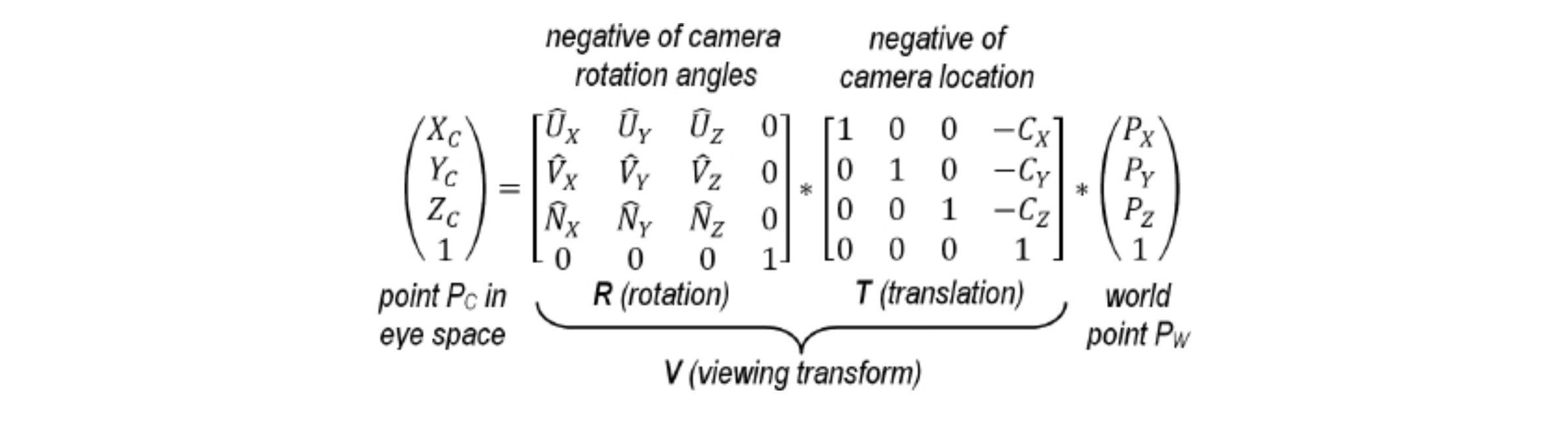
보통 V 행렬은 model 행렬 M과 연결되어 model-view 행렬 MV 행렬로 사용됩니다.
MV = V * M
Model Space에 있던 Pm이 Camera Space에 있는 Pc로 변환되는 과정은 다음과 같이 간단하게 나타낼 수 있습니다.
Pc = MV * Pm
이렇게 변환 행렬을 한 번에 계산하여 적용한다면 보다 간단하고 확장 가능한 계산이 가능해집니다.
'College Study > OpenGL' 카테고리의 다른 글
| (Draft) Managing 3D Graphics Data : Highlights & Codes (0) | 2022.03.10 |
|---|---|
| [그래픽스] 투영 행렬, Look-At 행렬, GLSL 변환 행렬 함수 (Projection Matrices, Look-At Matrices, GLSL Functions for Transformation Matrices) (0) | 2022.03.07 |
| [그래픽스] 기초 수학 (3) - 벡터 (0) | 2020.10.15 |
| [그래픽스] 기초 수학 (2) - Transformation Matrices (변환 행렬) (0) | 2020.10.15 |
| [그래픽스] 기초 수학 (1) - 좌표계, 점, 행렬 (0) | 2020.10.15 |



댓글