* Computer Graphics Programming in OpenGL with C++ 책을 참고하였습니다.
* 책을 번역한 것이 아닌, 제가 독학 후 책을 참고하여 설명하는 게시물입니다. 따라서 책에 없는 부연 설명이 있기도 하며, 의역 또는 오역, 오개념이 있을 수 있습니다. 피드백은 댓글을 남겨주세요.
* 영어 용어를 최대한 한국어로 번역하지 않습니다. 처음부터 코드에서 사용되는, 또는 원서나 인터넷에서 사용되는 보편적 용어를 사용하여 개념을 잡는 것을 추천드립니다.
지난 포스트에 이어, 3D 그래픽스 프로그램에서 수학을 사용하는 방식에 대해 설명하겠습니다.
그래픽스에서는, 물체의 변환을 수행하기 위해 행렬들이 사용됩니다. Translation(이동), Rotation(회전), Scale(축척), Projection(투영), Look-at 변환 행렬이 대표적인 행렬들입니다. 이 행렬들은 모두 4x4 크기의 행렬입니다. 이렇게 크기(차원)가 맞는 행렬이여야 임의로 행렬 계산을 결합할 수 있고, 미리 계산된 행렬 변환을 사용할 수 잇게 됩니다.
Translation
트랜슬래이션 행렬은 물체를 한 위치에서 다른 위치로 이동시키는 데 사용됩니다. 점(X, Y, Z)를 (TX, TY, TZ)만큼 이동시킨 점은 다음과 같이 구합니다. 이때, 점에 곱해진 행렬이 트랜슬래이션 행렬입니다.
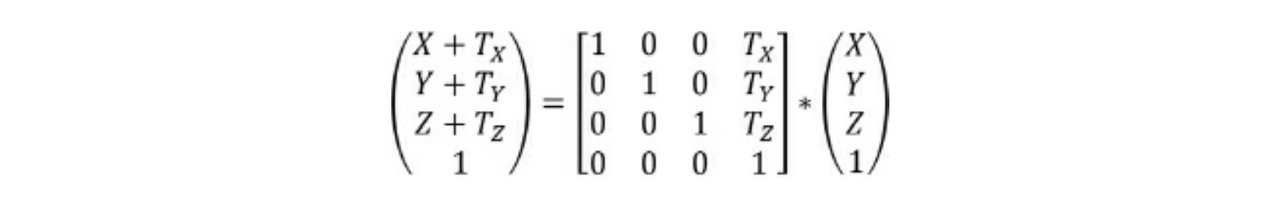
glm::translate(x, y, z) : (x, y, z)에 의해 이동되는 행렬을 만듭니다.
mat4 * vec4
Scaling
스캐일 행렬은 물체의 크기를 바꾸거나, 점들을 원점 가까이 (또는 멀리) 이동시킬 때 사용됩니다. (점의 배율을 조정해 점의 집합을 확장 또는 축소해야 점의 그룹으로 정의되는 OpenGL 개체를 키우거나 줄일 수 있습니다.) 점(X, Y, Z)를 (S, S, S)만큼 축척시킨 점은 다음과 같이 구합니다. 이때, 점에 곱해진 행렬이 스캐일 행렬입니다.
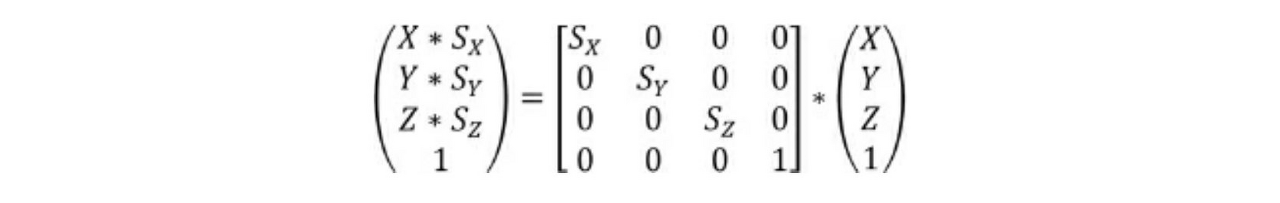
glm::scale(x, y, z)
mat4 * vec4
스캐일 행렬을 통해 오른손 좌표계와 왼손좌표계를 전환할 수도 있습니다. 다음 스캐일 행렬은 Z 좌표의 부호를 바꿔 좌표계를 전환합니다.

Rotation
로태이션 행렬은 약간 복잡합니다. 3D 공간에서 항목을 회전하려면 회전 축과 회전량을 각도 또는 radian으로 지정해야하기 때문입니다. 우리가 행렬로 전환하는 회전 방식은 오일러 각을 사용한 회전 방식입니다. 오일러 각을 간단히 정리하자면, 3D 물체의 회전은 X, Y, Z 세개의 회전 축과 회전량 조합으로 나타낼 수 있다는 이론입니다. 자세히 들어가자면 어려운 개념이니 다음을 참고하세요. 그림을 따라 그려보며 이해하는 것도 좋습니다.
오일러 각 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 오일러 각(Euler角, Euler angle)은 강체가 놓인 방향을 3차원 공간에 표시하기 위해 레온하르트 오일러가 도입한 세 개의 각도이다.[1] 즉, 3차원 회전군 SO(3)의 한 좌
ko.wikipedia.org
따라서 우리는 총 3번의 연산을 통해 회전을 정의합니다. 각각 X축, Y축, Z축을 기준으로 회전시킵니다.
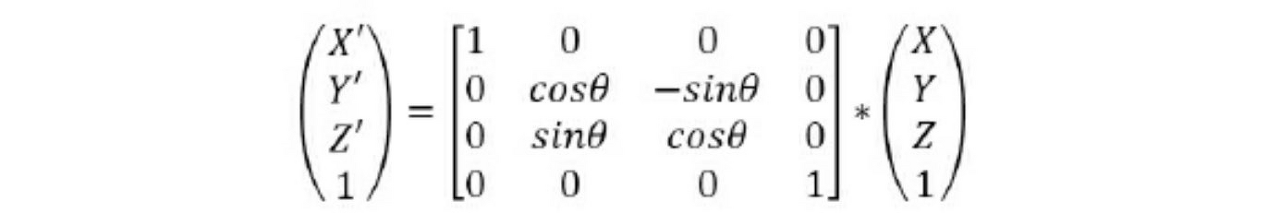
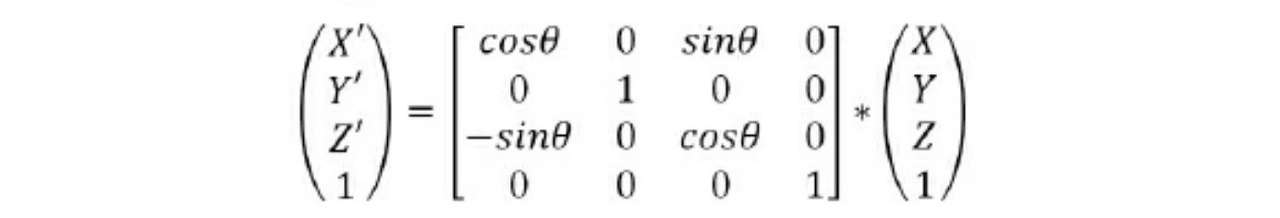

glm::ratate(mat4, θ, x, y, z)
mat4 * vec4
실제로 오일러 각을 사용하여 3D 공간에서 '원점을 지나지 않는' 축을 기준으로 물체를 회전시키려면 다음과 같은 과정이 필요합니다.
1. 원점을 지날 수 있도록 축을 이동 변환합니다.
2. X, Y, Z 축을 기준으로 적절한 오일러 각으로 회전합니다.
3. 1번의 이동 변환을 다시 반대로 해줍니다. (역변환)
위 세개의 변환식은 각각의 역 로태이션이 행렬의 전치와 동일합니다. 따라서 cos(-θ)=cos(θ), sin(-θ)=sin(θ)로 계산하여 변환 전 값을 찾을 수 있습니다. 이 속성을 기억하면 나중에 유용하니 참고하세요. 오일러 각은 일부 3D 그래픽 응용 프로그램에서 특정한 효과를 발생시키는 데 사용됩니다. 따라서 회전을 계산하는 데 quarternions를 사용하는 것이 좋지만, 일단은 오일러 각으로도 충분한 계산을 할 수 있으니 넘어가도록 하겠습니다.
다음 포스트에서는 '벡터'의 개념을 정리합니다.
'College Study > OpenGL' 카테고리의 다른 글
| [그래픽스] 공간(Local Space, World Space, Eye Space) 간 변환 (0) | 2022.03.02 |
|---|---|
| [그래픽스] 기초 수학 (3) - 벡터 (0) | 2020.10.15 |
| [그래픽스] 기초 수학 (1) - 좌표계, 점, 행렬 (0) | 2020.10.15 |
| [그래픽스] 정점으로 개체 그리기, 애니메이팅, 모듈화 (0) | 2020.06.09 |
| [그래픽스] 파일에서 GLSL 소스코드 읽기 (0) | 2020.06.08 |



댓글