https://youtu.be/nJyUyKN-XBQ?feature=shared
지난 동영상의 예제에서는 계산 그래프를 사용해 함수 $\mathcal{J}$를 계산해 보았습니다. 그 그래프를 다시 정리해서 그려 놓았는데, 어떻게 이를 이용해 함수 $\mathcal{J}$의 도함수를 계산하는지 알아봅시다.

계산 그래프입니다. $v$에 대한 $\mathcal{J}$의 도함수를 구해 봅시다. 무슨 뜻일까요? $v$의 값을 아주 조금 바꾸면 $\mathcal{J}$의 값이 어떻게 바뀌는지 묻는 것이죠. $\mathcal{J}=3v$라고 정의되어 있습니다. $v$는 11입니다. 따라서 11을 조금 증가시켜 11.001로 만들면, $\mathcal{J}=3v$이고 현재 33이므로 33.003으로 증가됩니다. $v$를 0.001 증가시켰더니 $\mathcal{J}$가 그 세 배 증가했으니까 $v$에 대한 $\mathcal{J}$의 도함수는 3입니다. $\mathcal{J}$의 증가량이 $v$의 증가량의 세 배이기 때문입니다.
지난 동영상에서 했던 것과 비슷합니다. $f(a) = 3a$였고, $\frac{df(a)}{da}$, 간단하게 $\frac{df}{da}$라고도 쓸 수 있는데 이는 3이었습니다. 여기서 $\mathcal{J}=3v$이므로 $\frac{d\mathcal{J}}{dv}$는 3입니다. $\mathcal{J}$가 $f$를 대신하고, $v$가 $a$를 대신하는 것입니다.
역전파는 이렇습니다. 이 마지막 출력값 변수의 $v$에 대한 도함수를 얻으면 역전파의 한 단계를 끝낸 것입니다. 그래프에서 한 단계 뒤로 가는 것이죠.
다른 경우를 살펴봅시다. $\frac{d\mathcal{J}}{da}$는 얼마일까요? $a$의 값을 증가시키면 $\mathcal{J}$의 값에 어떤 영향을 끼칠까요?
예제를 봅시다. 현재 $a$ = 5인데 5.001로 증가시켜 봅시다. $v = a + u$이고 이는 11이었으므로 11.001로 증가하고, $\mathcal{J}$는 33.003으로 증가합니다. $a$를 0.001만큼 증가시키면 $\mathcal{J}$는 0.003만큼 증가합니다. 증가한다는 것은 $a$의 변화가 계산 그래프의 오른쪽으로 전파되어 $\mathcal{J}$가 33.003이 된다는 뜻입니다. $\mathcal{J}$의 증가량은 $a$의 증가량보다 세 배 많고, 이는 도함수가 3이라는 뜻입니다.
이렇게 생각할 수도 있습니다. $a$를 바꾸면 $v$도 바뀌고, $v$를 바꾸는 것으로 $\mathcal{J}$도 바꿀 수 있다고 말입니다. $a$의 값을 조금 높였을 때 $\mathcal{J}$에 일어나는 전체 변화는 먼저 $a$를 바꾸면 $v$가 증가하고, 그 $v$의 변화가 $\mathcal{J}$를 증가시킵니다. 미적분에는 연쇄법칙이라는 것이 있습니다. 만약 $a$가 $v$에 영향을 끼치고, 그것이 $\mathcal{J}$에 영향을 끼친다면 $a$를 밀었을 때 $\mathcal{J}$의 변화량은 $a$를 밀었을 때 $v$의 변화량과 $v$를 밀었을 때 $\mathcal{J}$의 변화량의 곱입니다.
이 계산으로 알 수 있는 것은 $a$를 0.001만큼 바꾸면 $v$는 같은 양으로 바뀐다는 것입니다. 따라서 $\frac{dv}{da}$는 1입니다. 전에 계산해 놓은대로 $\frac{d\mathcal{J}}{dv}$ = 3이고, $\frac{dv}{da}$ = 1이므로 곱해보면 $\frac{d\mathcal{J}}{da}$ = 3입니다. 여기서 알 수 있는 것은 $\frac{d\mathcal{J}}{dv}$를 계산하는 것이 $\frac{d\mathcal{J}}{da}$를 계산하는 데 도움을 준다는 것입니다. 이것이 역방향 계산의 한 단계 중 하나입니다.
표기법 하나를 더 알아봅시다. 역방향 전파를 구현하는 코드를 작성할 때 보통 구하고자 하는 최종 출력값이 있을 텐데, 이 경우 그 최종 출력값은 $\mathcal{J}$입니다. 계산의 많은 부분이 $a$, $b$, $c$, $u$, $v$ 같은 여러 중간 변수를 포함해 $\mathcal{J}$의 도함수를 구하는 데 사용됩니다. 소프트웨어 구현에서는 변수의 이름을 짧게 하기 위해 d-이라고만 합니다. 예를 들어 $v$에 대한 도함수는 dv, $a$에 대한 도함수는 da라고 하는 것이죠. 이 값들은 각각 $\frac{d\mathcal{J}}{dv}$와 $\frac{d\mathcal{J}}{da}$를 의미합니다.
이제까지 역방향으로 계산해서 $dv = 3$, $da = 3$임을 구했습니다. 계속해서 도함수를 계산해 봅시다. $u$에 대해 알아보겠습니다. $\frac{d\mathcal{J}}{du}$는 얼마일까요? $u$를 6에서 6.001로 증가시키면, $v$는 11에서 11.001로 증가하고, $\mathcal{J}$는 33에서 33.003으로 증가합니다. 따라서 $\frac{d\mathcal{J}}{du} = \frac{d\mathcal{J}}{dv}\frac{dv}{du}=3 × 1 = 3$입니다. 코드에서는 이 값을 du라고 합니다.
마지막으로 $\frac{d\mathcal{J}}{db}$를 계산해 봅시다. 연쇄법칙에 따라 $\frac{d\mathcal{J}}{db} = \frac{d\mathcal{J}}{du}\frac{du}{db}$입니다. $b$를 3에서 3.001로 바꾸면, $u = bc$이므로 6에서 6.002로 증가합니다. 따라서 $\frac{du}{db} = 2$입니다. 이미 $\frac{d\mathcal{J}}{du}=3$을 구했으므로 곱하면 $\frac{d\mathcal{J}}{db} = 6$입니다. 코드에서는 db = 6입니다.
마지막 계산 $\frac{d\mathcal{J}}{dc} = \frac{d\mathcal{J}}{du}\frac{du}{dc}$도 마찬가지로 3 × 3 = 9가 되어, dc = 9입니다.
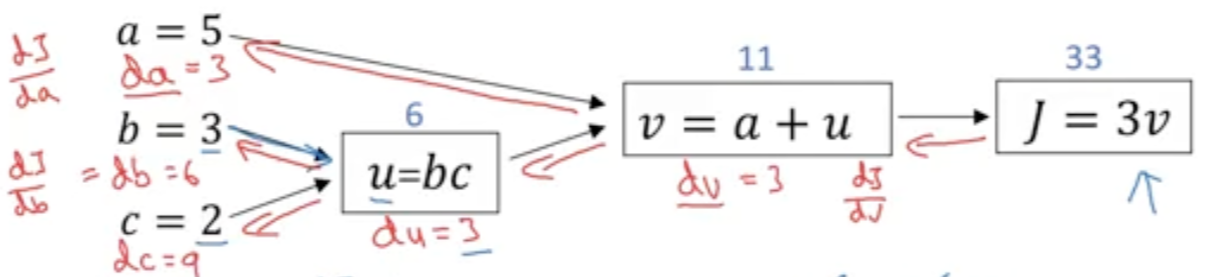
이 동영상에서 얻어가야 할 핵심은 다음과 같습니다. 도함수를 계산할 때 가장 효율적인 방법은 계산 그래프를 따라 오른쪽에서 왼쪽으로, 즉 역방향으로 진행하는 것입니다. 먼저 마지막 변수에 대한 도함수를 구하고, 그것을 사용해 이전 변수들에 대한 도함수를 차례로 계산합니다. 정방향 계산은 최종 출력값 $\mathcal{J}$를 구하는 과정이고, 역방향 계산은 $\mathcal{J}$에 대한 각 변수들의 도함수를 구하는 과정입니다. 이를 통해 최적화나 경사 하강법에 필요한 값들을 효율적으로 얻을 수 있습니다.




댓글