https://youtu.be/hCP1vGoCdYU?feature=shared
전에 신경망의 계산은 이렇게 나눌 수 있다고 했었습니다. 정방향 패스, 정방향 전파는 신경망의 출력값을 계산하고, 이는 역방향 패스, 역방향 전파로 이어져 경사나 도함수를 계산합니다. 계산 그래프를 보면 왜 이렇게 나누는지 알 수 있는데, 이번 동영상에서는 그 예제를 살펴보도록 하겠습니다.
계산 그래프에 대해 설명하기 위해 로지스틱 회귀나 완성된 신경망보다 더 쉬운 것을 예로 들어 봅시다. 함수 $\mathcal{J}$를 계산한다고 해 보죠. 이 함수는 변수 세 개 $a$, $b$, $c$를 가지고 있습니다. 이 함수는 $3(a + bc)$입니다.
$\mathcal{J}=3(a+bc)$
이 함수를 계산하는 데에는 서로 다른 세 단계의 과정이 필요합니다. 먼저 $bc$를 계산해야 합니다. 이를 $u$라는 변수에 저장해서 $u = bc$라고 합시다.
다음에 $v = a + u$라고 할 때 $v$를 계산해야 합니다. 마지막으로 출력값 $\mathcal{J} = 3v$입니다. 이것이 함수 $\mathcal{J}$의 계산입니다. 이것이 계산하려고 했던 함수 $\mathcal{J}$의 마지막이죠.
위의 세 단계를 다음과 같이 계산 그래프로 나타낼 수 있습니다. 세 변수 $a$, $b$, $c$를 여기에 그립니다.
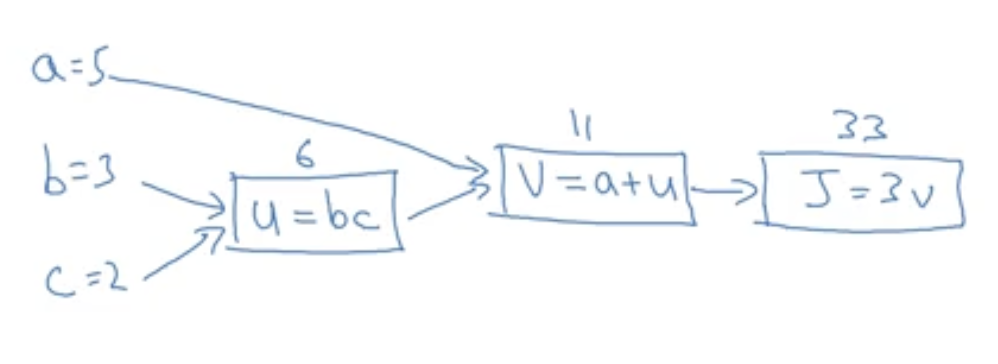
처음으로 계산할 것은 변수 $u = bc$입니다. 사각형 안에 넣고, 이것의 입력값은 $b$와 $c$입니다. 다음에 $v = a + u$가 있겠죠. 이것의 입력값은 $u$와 $a$입니다. 그리고 마지막으로 $\mathcal{J} = 3v$가 있습니다.
예를 들어 $a$가 5, $b$가 3, $c$가 2라고 한다면, $u = bc$는 6입니다. $v = a + u$는 5 + 6이니까 11이고, $\mathcal{J}$는 그 세 배인 33입니다. 확인해 보면 알겠지만 3(5 + 3×2)는 33이 맞습니다.
계산 그래프는 $\mathcal{J}$ 같은 특정한 출력값 변수를 최적화하고 싶을 때 유용합니다. 그리고 로지스틱 회귀의 경우에 $\mathcal{J}$는 당연히 최적화할 비용 함수입니다. 이 예제에서 확인할 수 있는 것은 왼쪽에서 오른쪽의 패스로 $\mathcal{J}$의 값을 계산할 수 있다는 것입니다.
다음 강의에서는 도함수를 구하기 위해 오른쪽에서 왼쪽으로 패스하는 것을 알아볼 것입니다. 이렇게 파란 화살표의 반대 방향으로 가는 것이죠. 도함수를 계산하는 가장 자연스러운 방법입니다. 정리해 보면 계산 그래프는 왼쪽에서 오른쪽으로 계산하는 파란색 화살표를 사용해 계산을 정리하였습니다. 다음 동영상에서는 역방향으로 빨간색 화살표를 이용해 오른쪽에서 왼쪽 방향으로 도함수를 계산해 보겠습니다.




댓글