https://youtu.be/z_xiwjEdAC4?si=lQypGk0marGIIarD
이번 동영상에서는 로지스틱 회귀의 경사 하강법을 구현하는 데 필요한 도함수를 계산하는 방법에 대해 알아보겠습니다.
여기서 알고 가야 할 것은 로지스틱 회귀의 경사 하강법을 위해 필요한 핵심 공식을 구현하는 방법입니다. 이 동영상에서는 이를 계산 그래프를 통해 하려고 합니다. 계산 그래프를 로지스틱 회귀의 경사 하강법에 사용하는 것은 조금 과하긴 하지만, 이런 방법을 사용해 설명하면 이런 개념이 익숙해져서 나중에 완전한 신경망을 다룰 때 이해가 더 잘 될 것입니다.
$z = w^Tx+b$
$\hat{y}=a=\sigma(z)$
$\mathcal{L}(a,y)=-(y\log(a)+(1-y)\log(1-a))$
그러면 로지스틱 회귀의 경사 하강법에 대해 알아봅시다. 다음과 같은 로지스틱 회귀를 복습해 봅시다. $y$의 예측값은 이렇게 정의하고, 그 안에 있는 $z$의 정의는 이렇습니다. 그리고 샘플 하나만 생각할 때 그 하나의 샘플에 대한 손실 함수는 이렇습니다. 여기서 $a$는 로지스틱 회귀의 출력값이고 $y$는 참 값 레이블입니다.
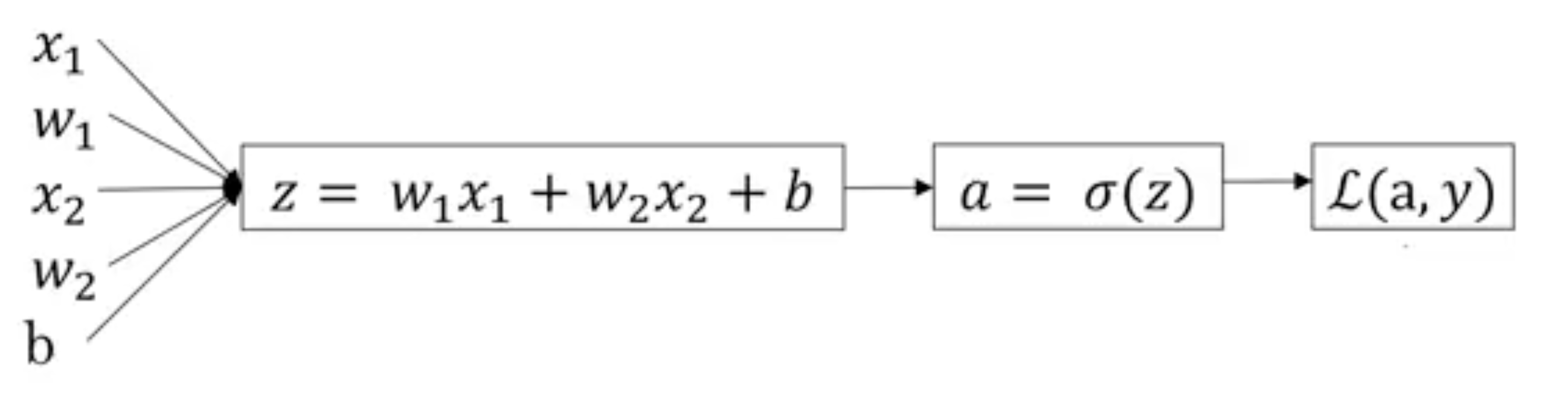
그러면 이것을 계산 그래프로 나타내 봅시다. 이 예제에서는 특성이 $x_1$과 $x_2$ 두 개라고 하겠습니다. $z$를 계산하려면 특성값 $x_1$과 $x_2$를 포함해 $w_1$, $w_2$, $b$도 필요합니다. 계산 그래프에서는 이 모두가 $z$를 계산하는 데 필요합니다. $z = w_1x_1 + w_2x_2 + b$입니다.
이걸 사각형 안에 넣고, 그 다음엔 $\hat{y} = a = \sigma(z)$를 계산합니다. 이게 계산 그래프에서의 다음 단계이고, 마지막으로 $\mathcal{L}(a, y)$를 계산합니다. 식을 다시 쓰진 않겠습니다. 로지스틱 회귀에서의 목적은 매개변수 $w$와 $b$를 변경해서 이 손실을 줄이는 것입니다.
단일 훈련 샘플에 대한 손실의 계산에 대해서는 예전에 보았습니다. 이제 반대 방향에서 도함수의 계산에 대해 이야기해 봅시다. 그래프를 깔끔하게 만들어 보았습니다. 구하고자 하는 것은 이 손실 함수의 도함수이니까 역방향으로 가서 $a$에 대한 손실 함수의 도함수를 계산해 봅시다. 코드에서는 이 변수를 da라고 나타낼 수 있습니다.
미적분에 대한 지식을 이용하여 이를 계산하면 다음과 같은 결과가 나옵니다. $-(y/a) + ((1 - y)/(1 - a))$. 미적분을 잘 알아서 손실 함수의 식을 가지고 $a$에 대한 도함수를 계산해보면 이런 결과가 나옵니다. 미적분을 잘 알지 못해도 괜찮습니다. 강의에서 필요한 도함수의 식은 항상 알려드리도록 하겠습니다.
미적분을 잘 안다면 지난 슬라이드에서 손실 함수의 식을 보고 직접 $a$에 대한 도함수를 계산해 보는 걸 추천합니다. 하지만 미적분에 대해 잘 알지 못한다면 상관없습니다. $a$에 대한 최종 출력값의 도함수인 $da$를 계산했으니 이제 역방향으로 더 갈 수 있습니다.
계산해 보면, 파이썬 코드 변수 이름 dz는 $z$에 대한 손실 함수의 도함수이고, $\mathcal{L}$을 $a$와 $y$에 대한 손실이라고 직접 써도 좋습니다. 두 표기법 모두 괜찮습니다. 그러면 이는 $a - y$라고 나타낼 수 있습니다. 미적분을 잘 알고 있다면 이렇게 이해할 수 있습니다. 그렇지 않다면 신경 쓰지 마세요.
$\frac{dL}{dz}$는 $\frac{d\mathcal{L}}{da}\frac{da}{dz}$라고 나타낼 수 있는데, 계산해 보면 $\frac{da}{dz}$는 $a(1 - a)$이고, $\frac{d\mathcal{L}}{da}$는 방금 이것이라고 계산했습니다. 그래서 $\frac{d\mathcal{L}}{da}$인 이 항과 $\frac{da}{dz}$인 이 항을 서로 곱하면 식을 $a - y$로 간단히 할 수 있습니다. 잠깐 설명했던 연쇄법칙을 사용해 이렇게 도함수를 구한 것입니다.
미적분을 할 줄 알면 직접 계산해 보아도 좋고, 그렇지 않다면 그냥 $\frac{d\mathcal{L}}{da} = a - y$라고 알고 있으면 됩니다.
역방향 전파의 마지막 단계는 $w$와 $b$를 얼마나 바꾸어야 하는지 계산하는 것입니다. 예를 들어 $w_1$에 대한 도함수는 코드에서는 $dw_1$이라고 나타내고, $x_1$$dz$와 같으며, $w_2$의 변화량을 나타내는 $dw_2$는 $x_2dz$와 같습니다. 그리고 $db = dz$입니다.
단일 샘플에 대해서만 경사 하강법을 사용한다면 이렇게 할 수 있습니다. 이 식을 사용해 d$z$를 계산하고, 이 식들로 $dw_1$, $dw_2$, $db$를 계산한 후 이렇게 갱신합니다. w_1 := w_1 - (alpha)dw_1. w_2는 똑같이 하면 되고, b := b - (alpha)db입니다. 이것은 단일 샘플에 대한 경사 하강법의 한 단계입니다.
도함수를 계산하고 단일 샘플에 대한 로지스틱 회귀의 경사 하강법을 구현하는 방법을 알아보았습니다. 하지만 로지스틱 회귀 모델을 훈련시키려면 단일 샘플이 아니라 $m$개의 훈련 샘플을 가진 훈련 세트 전체를 훈련해야 합니다. 다음 동영상에서는 이것을 가지고 단일 샘플이 아닌 훈련 세트 전체를 학습시키는 방법을 알아보도록 합시다.




댓글